Solar flares, the most powerful magnetic explosions in our solar system, are often accompanied by intense bursts of radio emission known as type III solar radio bursts. These bursts provide valuable clues about the acceleration and transport of energetic electrons in the Sun’s atmosphere and beyond. Understanding these bursts is not only crucial for solar physics but also for predicting space weather events that can disrupt our technological infrastructure. A key question surrounding type III bursts has been the beams of energetic electrons, which are believed to be responsible for the radio emission, travel vast distances from the Sun (e.g. Ginzburg & Zhelezniakov, 1958). The relaxation of the electron beam over the short distance in contrast to large beam-travel distances observed is often referred to as Sturrock’s dilemma (Sturrock, 1964).
A new research paper by Kontar et al 2024 incorporates a crucial element often overlooked in previous studies: the finite spatial size of the electron cloud and the consequent spatial variability of the quasilinear relaxation process. The standard approach assumes that this quasilinear relaxation is uniformly fast throughout the space (e.g. Ryutov, & Sagdeev, 1970, Melnik, V. N. et al, 1999). However, this assumption is too simplistic. Kontar et al 2024 point out that the rate of quasilinear relaxation depends on the density of the electron beam itself. Since the beam’s density naturally varies across its lengths, the relaxation process will also vary.
Nonlinear Diffusion
This spatial variation in relaxation leads to a new concept in the model: nonlinear diffusion. Diffusion, in general, describes the spreading out of particles from a region of higher concentration to a region of lower concentration. In the context of the propagating electron beam, it refers to the beam’s spatial expansion as it travels away from the Sun. The “nonlinear” aspect comes from the fact that the diffusion coefficient, which quantifies the rate of this spreading, is not constant but depends on the local density of the electron beam. Specifically, the diffusion is faster in regions where the beam density is lower and slower in regions where the density is higher. This is because a lower electron density leads to slower quasilinear relaxation and hence faster diffusion, while a higher electron density leads to faster relaxation and slower diffusion. The advection-nonlinear diffusion equation with $n(x,t)$ normalised with $n_b$ can be written
$$\frac{\partial n}{\partial t}+\frac{v_0+v_{min}}{2}\frac{\partial n}{\partial x}-\frac{\partial}{\partial x}D_{xx}^0\frac{n_{b}}{n}\frac{\partial n}{\partial x}=0\,,$$
where the nonlinear dependency of $D_{xx}$ on $n(x,t)$ is explicitly highlighted by introducing $D_{xx}=D_{xx}^0\frac{n_{b}}{n}$.

Figure 1: AI-generated image inspired by the non-linear-diffusion advection model.
Super-Diffusion: Ballistic Expansion of the Electron Beam
The solution to this equation reveals that the electron beam undergoes super-diffusion. The evolution of an electron beam given by initial condition
$$n(x,t=0)=n_b\delta \left( x/d\right)\,,$$
where $n_b$ is the electron beam density and $d$ is the characteristic size, can be written
$$n(x,t)=\left(\frac{\left(x-{(v_0+v_{\min})}t/{2}\right)^2}{2D^0_{xx}n_{b}t} +\frac{2\pi^2}{n_bd^2}D^0_{xx}t\right)^{-1}$$
This means that the beam expands much faster than it would under standard diffusion. Instead of the beam’s width increasing with the square root of time (as in normal diffusion), it increases linearly with time – a behavior known as ballistic expansion.
This super-diffusion is a direct consequence of the nonlinear nature of the diffusion. The faster diffusion in the lower-density regions of the beam causes it to spread out more rapidly than expected. The electron density and the spectral energy density of Langmuir waves tend to decrease with distance from the Sun. To validate the model, we compare the analytical solution with the results of numerical simulations of the full kinetic equations, carried out in previous studies (Figure 2).
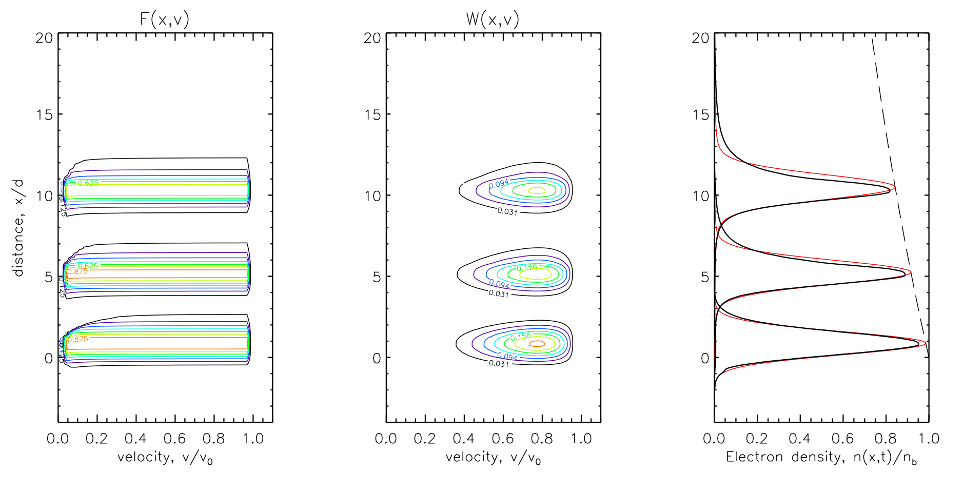
Figure 2: Simulated electron distribution ($f(v,x,t)$) (left), spectral energy density ($W(v,x,t)$) (center), and electron beam density ($n(x,t)$) (right) at three time moments $t=0.5, 3, 6$ s for the following beam-plasma parameters $n_b=120$ cm$^{-3}$, $n_p=6\times 10^8$ cm$^{-3}$ (i.e. $f_{pe}\simeq 220$ MHz) and $v_0=10^{10}$ cm/s, $v_{\min}=0.1v_0$, $d=3\times10^9$ cm. The dashed line shows the decrease of the peak density.
Conclusions
The solution allows to investigate large-scale evolution of electron beam and Langmuir waves and quantitively explains the numerical simulation results. In application to type III solar radio bursts, the spectral energy density of plasma emission via Langmuir waves depends on the beam density and would decrease inversely with distance, which is required to explain the radial type III solar burst flux variations (Krupar et al. 2014). The spatial expansion of the beam is also qualitatively better fit for the time width of type III bursts (Reid & Kontar 2018).
Based on the recent paper by Eduard P. Kontar, Francesco Azzollini, and Olena Lyubchyk, The Astrophysical Journal, 976 233 (2024). DOI: 10.3847/1538-4357/ad8560
References:
Ginzburg, V. L., & Zhelezniakov, V. V. 1958, SvA, 2, 653
Kontar et al, 2024, ApJ, 976, 233
Krupar et al, 2014, Solar Physics, 289, 3121
Melnik, V. N. et al, 1999, Solar Physics, 184, 353
Reid & Kontar, 2018, Astronomy & Astrophysics, 614, A69
Ryutov, & Sagdeev, 1970 JETP, 31,396
Sturrock, P. A., 1964, Proceedings of the AAS-NASA Symposium, p357

